Nicolás
de Oresme, filósofo y matemático francés, fue hacia 1350 el primero en señalar
la divergencia de la serie armónica. A él se
atribuye la metáfora, ciertamente poética, que compara a las series divergentes
con los ángeles de Dios, ya que vuelan aproximándose siempre a la eternidad, al
infinito…
Pero,
¿qué son las series divergentes? Consideremos como ejemplo más sencillo, la
serie de los números enteros positivos: 1, 2, 3, 4… Si los vamos sumando y cada
año agregamos un número a la serie: 1+2+3+4, esta suma después de los primeros
cuatro años, dará como resultado 10. Ahora bien, si transcurre un número
infinito de años, la suma de la serie llega al infinito. Los matemáticos dieron
en llamar a esas series “divergentes” porque con un número infinito de
términos, se disparan hasta el infinito.
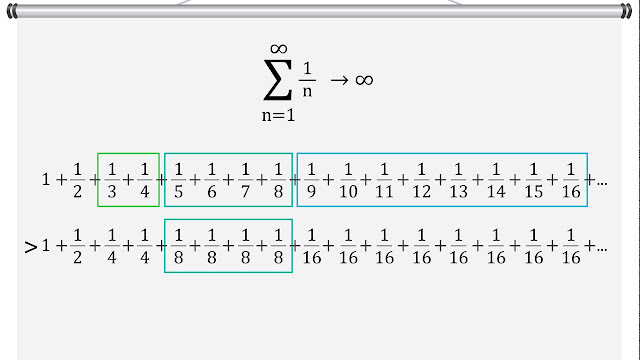
Existen series divergentes que, aunque también se dirigen al infinito, lo hacen de una forma cada vez más lenta. Para Nicolás de Oresme, serían ángeles con alas mucho menos vigorosas, sí, pero cuyo destino final es igualmente infinito. Consideremos ahora la serie armónica, primer ejemplo célebre de serie divergente cuyos términos se aproximan cada vez más a cero: 1, ½, 1/3, ¼… En caso de que sumemos los términos: 1+1/2+1/3+1/4+… su crecimiento será tan pausado que si agregamos un término cada año, después de 1043 años la suma total no llegará a 100. Pero atención, si bien crece cada vez más lentamente, su destino final es alcanzar también el infinito. Su fórmula y su desarrollo son los siguientes:
Los
matemáticos y los científicos familiarizados con los números y su
comportamiento, tienden a olvidar lo asombroso que este descubrimiento puede
resultar para los estudiantes que comprenden el fenómeno por primera vez. Es
una fantástica metáfora real de la inmensidad que habita en lo diminuto, una
inmensidad tan grande que de hecho, es infinita.
Perdida
durante siglos la obra de Oresme, fue recuperada por el matemático italiano
Pietro Mengoli, que en 1647 volvió a encontrar la solución. Ya a finales de
aquel siglo XVII los hermanos Bernoulli, Johann y Jakob, publicaron una
demostración en términos más modernos en su Tratado
sobre las series infinitas, obra de 1689.
Conviene
tener presente que el concepto de infinito,
aunque intuitivamente podamos alcanzarlo, no resulta fácil de demostrar de
forma matemática. En tratados tanto de matemáticas, como de física o filosofía,
se habla a veces de “infinitos grandes” e “infinitos pequeños”, lo que resulta
muy poco racional. El asombroso mundo de la serie armónica se ajusta mucho
mejor a la realidad de nuestro universo físico y las leyes que lo rigen, puesto
que introduce la idea de velocidad en
la progresión de las series. El espacio-tiempo afecta a las series numéricas
del mismo modo que afecta al resto de cuanto forma parte del universo físico. Lo
tangible y lo intangible. Meditad un momento sobre ello.
-Mamá, ¿por qué todos los chinos parecemos iguales?
-Yo
no soy tu mamá.




No hay comentarios:
Publicar un comentario